Der ursprünglich für die Messungen vorgesehene Kleinmaschinenprüfstand erweist sich als nicht geeignet. Die Drehmomentanzeige hat zwar einen maximalen Ausschlag von 5 Nm, der Antriebsmotor ist aber nicht für diese Belastung ausgelegt, so daß bereits bei einer Drehzahl von 200 U/min in der Antriebsmaschine der Ankernennstrom fließt.

Für die Messungen wird kurzfristig ein Meßplatz eingerichtet, der die benötigte Antriebsleistung aufbringt.

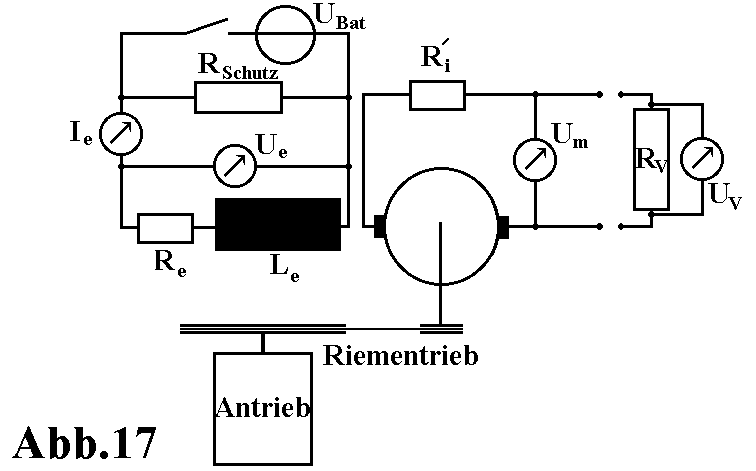
Die Abbildung 17 zeigt den Aufbau des Versuchsplatzes. Über einen Riementrieb wird die Versuchsmaschine angetrieben. Der Antrieb ist mit einer Waage, die das Antriebsmoment anzeigt gekoppelt. Die Übersetzung des Riementriebes beträgt ü=3,833, so daß das angezeigte Moment 3,833 mal größer ist als das tatsächliche Antriebsmoment. Die Drehzahl wird über einen Drehzahlmesser von der Antriebswelle abgegriffen. Die Erregerspule wird von der Batterie U_Bat gespeist. Um den Lichtbogen beim Ausschalten klein zu halten, ist parallel zur Erregerspule ein Feldschutzwiderstand geschaltet. Der Shunt RV, der als Belastung dient, ist nur bei der Belastungsmessung an die Versuchsmaschine angeschlossen. UV ist die Meßspannung, die im Leerlauf der induzierten Spannung Ui entspricht.

Der ohmsche Widerstand der Spule ist abhängig von der Temperatur der Kupferwicklung. Die Messung von Gleichstrom I und Gleichspannung U zu verschiedenen Zeitpunkten nach dem Einschalten gibt Aufschluß über den Widerstand und die Temperatur in Abhängigkeit von der Zeit.

Der Widerstand R der Spule beträgt bei einer beliebigen Temperatur J

(55)

Damit läßt sich die mittlere Temperatur der Spule zu einem beliebigen Zeitpunkt berechnen

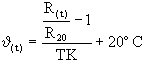(56)

mit dem Widerstand bei 20°C R20 und Temperaturkoeffizienten von Kupfer TK=0,0039K-1.

R20 ist die Temperatur beim Einschalten zum Zeitpunkt t=0s.

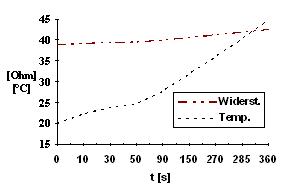
Tabelle 1 zeigt die gemessenen und berechneten Werte, in Diagramm 1 ist der Verlauf von Widerstand und Temperatur in Abhängigkeit von der Zeit aufgetragen.

Tabelle 1                                                                  Diagramm 1

Der Vergleich mit der Berechnung in Abschnitt 2.2.1 Gleichung (19) zeigt, daß der tatsächliche Widerstand der Spule zu Beginn der Messung bei t=0 etwas kleiner ist als der berechnete Wert. Der Grund dafür ist in der Raumtemperatur des Labors zu sehen, die nicht bei 20°C, sondern etwas darunter liegt.

Um die Induktivität berechnen zu können, wird der Scheinwiderstand Z gemessen, indem

die Spule mit 225 V Wechselspannung gespeist wird. Die Spule ist als eine Reihenschaltung aus ohmschem Wirkwiderstand und induktivem Blindwiderstand anzusehen. Der gemessene Betrag des Scheinwiderstandes Z ist dann

. (57)

Bei Netzfrequenz von 50 Hz und dem bekannten ohmschen Wirkwiderstand R» 40W läßt sich daraus die Induktivität L der Spule berechnen

. (58)

Die Messung zeigt eine erhebliche Abweichung von dem berechneten Wert in Abschnitt 2.3.1 Gleichung (38). Die Ursache liegt in den Vereinfachungen, die für die Berechnung angenommen wurden.

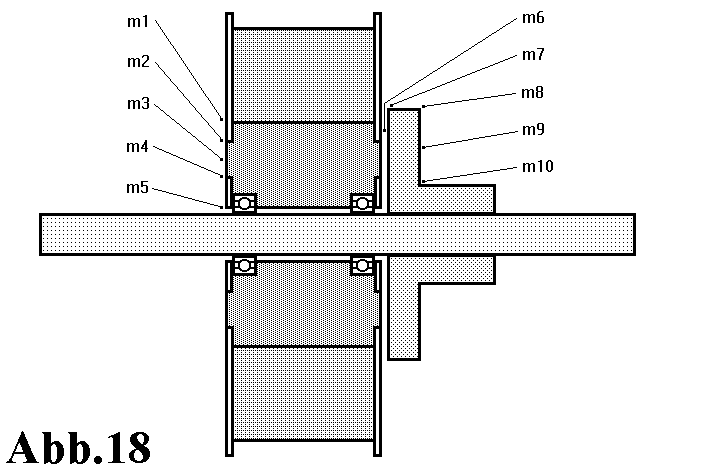
Die Induktion der magnetische Flußdichte, die von der Spule erregt wird, läßt sich mit einer Hall-Sonde messen. In der Abbildung 18 sind die Meßpunkte m1 bis m10 eigetragen, an denen die Induktion gemessen wurde. Die Hall-Sonde wird so in das Feld eingebracht, daß die Anzeige den maximalen Ausschlag in diesem Meßpunkt zeigt. Tabelle 2 zeigt die Messergebnisse für die Erregerströme Ie=3A, 4A und 5A.

Tabelle 2

Es zeigen sich im Vergleich mit den Ergebnissen der FEMAG-Berechnungen in Abschnitt 2.3.1, die in den Diagrammen dagestellt sind, gute Übereinstimmungen.

Bevor mit den vorgesehenen Versuchen begonnen werden kann, muß die Versuchsmaschine ausgewuchtet werden. Wie bereits in Abschnitt 2.2.3 beschrieben, ist eine Unwucht als Massenverschiebung gegenüber der Drehachse anzusehen. Bei der Versuchsmaschine besteht diese Massenverschiebung hauptsächlich aus der Wicklung, die durch das Einlöten der Kupferlitze am Umfang zu einer Seite ausgewölbt ist. Um die Unwucht auszugleichen, werden Schrauben und Gewindestangen auf der gegenüberliegenden Seite der Unwucht angebracht.

Die genaue Lage und Größe der Gewichte läßt sich mit einem elektronischen Auswuchtgerät bestimmen. Diese von der Firma Behnke durchgeführte Messung besteht hauptsächlich aus einer Schwingungsaufnahme während des Rotierens bei verschiedenen Drehzahlen. Zwei Schwingungsaufnehmer an den Lagerböcken und ein optischer Drehzahl- und Drehwinkelaufnehmer nehmen die Meßwerte auf und auf einer Anzeige und bei Bedarf durch einen Ausdruck wird Größe und Lage des Gegengewichts angezeigt. Nach dem Anbringen des Gewichts wird die Messung wiederholt und die Veränderungen der Schwinggeschwindigkeit kann beurteilt werden.

Der in Bild 10 abgebildete Ausdruck zeigt die Effektivwerte der Schwinggeschwindigkeiten und deren Richtung bei Meßläufen ohne Ausgleichsgewicht und mit 7,7g Ausgleichsgewicht bei 0°. Als Ergebnis wird empfohlen, ein Gewicht von 51,1g bei 17° anzubringen (Die Gewichtsangaben auf dem Ausdruck sind jeweils durch zehn zu dividieren).
         Bild 10

Nach dem Anbringen von 57,8g durch zwei Gewindestangen mit Muttern verringert sich die Schwingung auf 0,06 mm/s bei 288°.

Die Bilder 11 bis 13 zeigen verschiedene Analysen, die nach dem Auswuchten durchgeführt wurden. Der Schwingungsaufnehmer an der Antriebsseite ist mit 1 bezeichnet.

Bild 11 bis 13

Bei der Leerlaufmessung fließt kein Strom durch die Induktionsscheibe und die Kohlebürsten, es entsteht kein Spannungsfall und die an den offenen Klemmen gemessene Spannung ist gleich der induzierten Spannung Ui.

Bei verschiedenen Drehzahlen wird die Spannung zwischen den Sammelschienen mit stehender und rotierender Erregung gemessen. Zu jeder Drehzahl wird zusätzlich das Gegenmoment Mg aufgenommen (Tabelle 3).

Tabelle 3

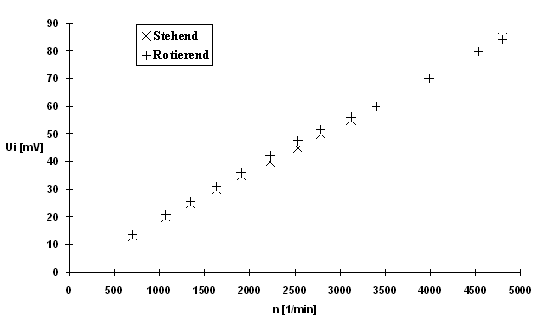
Das Diagramm 2 zeigt die Funktion Ui=f(n) bei den beiden Erregerarten.

Diagramm 2

Es ist deutlich zu sehen, daß die induzierte Spannung nicht abhängig von der Erregerart ist. Wie erwartet ist nach Gleichung (11) die induzierte Spannung linear abhängig von der Drehzahl.

Das Diagramm 3 stellt die Funktion Mg=f(n) dar:

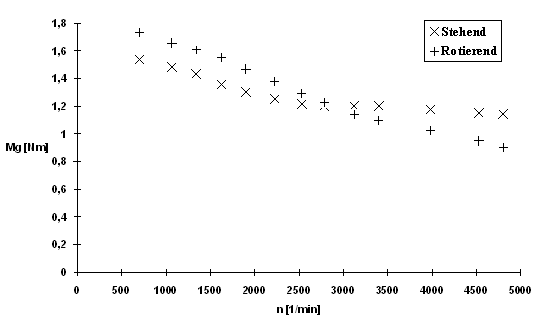
Diagramm 3

Das Gegenmoment, welches hauptsächlich aus der Bürstenreibung resultiert, wird mit zunehmender Drehzahl kleiner. Dieses Verhalten ist auf den Reibkoeffizienten der Kohlebürsten zurückzuführen, der mit wachsender Drehzahl kleiner wird.

Das Gegenmoment ist bei stehender Erregung für hohe Drehzahlen größer als das bei rotierender Erregung. Dies ist dadurch zu erklären, daß sich durch die konstruktionsbedingten Unregelmäßigkeiten des Eisenkerns (Schrauben, Bohrungen) ein radial inhomogenes Magnetfeld ausbildet. Es entstehen Wirbelströme, deren Gegenmoment quadratisch mit der Drehzahl wächst. Da diese Wirbelstromgegenmomente zwischen Induktionsscheibe und Erregerspule angreifen, können sich bei mitrotierender Erregung keine Wirbelströme ausbilden.

Das Gegenmoment bei niedrigen Drehzahlen mit rotierender Erregung ist größer als das bei stehender Erregung. Die Ursache macht die Meßreihe in Tabelle 4 deutlich. Es wird mit stehender und rotierender Erregung jeweils bei ein- und ausgeschalteter Spule das Gegenmoment gemessen.

Tabelle 4

Das Diagramm 4 stellt die Funktion Mg=f(n) mit stehender und rotierender Erregung bei Ie=0A und Ie=5A dar.

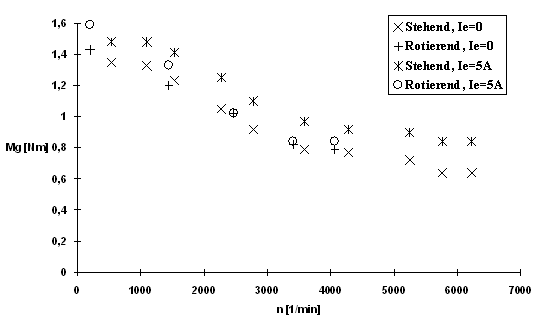
Diagramm 4

Wie zu sehen ist, wirkt sich bei stehender Erregung die eingeschaltete Erregung widerum durch das Wirbelstrombremsmoment aus. Bei rotierender Erregung ist bei niedrigen Drehzahlen eine Differenz zwischen dem Betrieb mit ein- und ausgeschalteter Erregung zu erkennen, die bei höheren Drehzahlen verschwindet. Ursache dafür ist möglicherweise die Feldverzerrung, die aus der Umgebung mit hoher Permeabilität (Fundament) resultiert.

Die folgende Meßreihe zeigt den Verlauf der induzierten Spannung bei verschiedenen Erregerströmen. Die Tabelle 5 beinhaltet die Meßreihen bei rotierender Erregung mit Ie=0,95A und Ie= 3A. Im Diagramm 5 sind diese Meßwerte als Funktion Ui=f(n) aufgetragen.

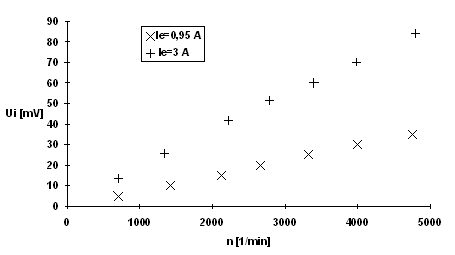
Tabelle 5                                                   Diagramm 5

Wie erwartet, ist nach Gleichung (11) die induzierte Spannung linear abhängig von der magnetischen Flußdichte und bei Verdreifachung des Erregerstromes verdreifacht sich die Steigung der Geraden ebenfalls. Dieses trifft nur solange zu, bis die Sättigung des Eisens erreicht ist, denn dann wächst die Induktion nicht mehr linear mit dem Erregerstrom.

Um festzustellen, bei welchem Erregerstrom die Sättigung erreicht ist, wird bei einer konstanten Drehzahl der Erregerstrom bis zur Belastungsgrenze von 8,5 A erhöht und die induzierte Spannung gemessen.

Die Belastungsgrenze der Erregerspule ist durch die Verlustleistung in der Wicklung gegeben. Bei einem Erregerstrom von 8,5 A wird die Temperatur nach kurzer Zeit so hoch, daß der Kunstharz weich wird.

Die Tabelle 6 zeigt die Meßwerte bei einer Drehzahl von 5385 1/min, das Diagramm 6 die Funktion Ui=f(Ie).

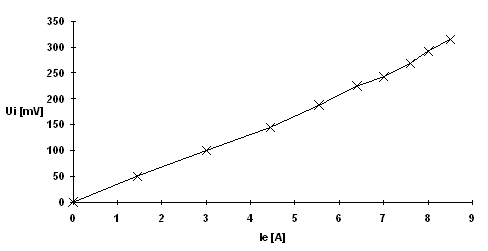
Tabelle 6                                                   Diagramm 6

Das Diagramm 6 läßt erkennen, daß bei einem Erregerstrom von 8,5 A die Sättigung des Eisenkerns noch nicht erreicht ist.

Als Belastung dient ein 600A Shunt, in dem die elektrische Leistung in Wärme umgewandelt wird. Über den Spannungsfall am Shunt kann der durch den Shunt fließende Strom berechnet werden. Aus den Leerlaufmessungen ist die induzierte Spannung bei entsprechender Drehzahl bekannt. Unter der Annahme, daß sich die induzierte Spannung bei Belastung nicht verändert, kann über die Differenz zwischen Spannungsfall am Shunt und induzierter Spannung der Spannungsfall über den inneren Widerstand Ri´ berechnet werden und mit dem fließenden Strom dann der Widerstand selbst. In Tabelle 7 sind die Meßwerte für die Drehzahl n und den Strom durch den Shunt Iv bei rotierender Erregung mit einem Erregerstrom von 5A aufgeführt.

Das Diagramm 7 stellt die Funktion Us=f(n) dar.

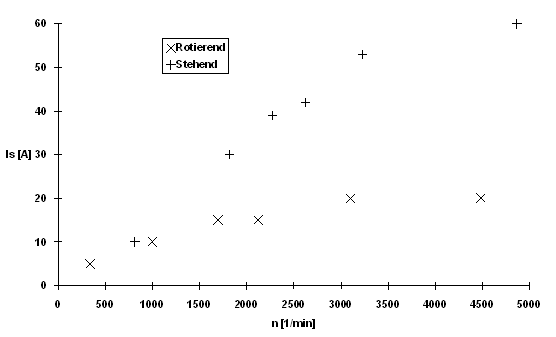
Tabelle 7

Diagramm 7

Auffällig am Verlauf der Kurven ist zum einen die große Differenz zwischen den beiden Erregerarten und zum anderen der geringe Bemessungsstrom.

Die Differenz zwischen beiden Kurven ist nicht konkret zu erklären. Da die induzierte Spannung in beiden Fällen gleich ist, muß davon ausgegangen werden, daß der fließende Strom in der Induktionsscheibe die Anordnung in Abhängigkeit der Erregerart verändert. Möglicherweise ist die Differenz aber auch auf den Bürstenübergangswiderstand zurückzuführen. Zu Beginn der Messungen waren die Bürsten mit Schleifpapier eingeschliffen worden. Die Oberfläche der Bürsten war daher nicht glatt, sondern rauh. Durch längeren Betrieb werden die Bürstenoberflächen glattgeschliffen, was einen geringeren Übergangswiderstand zur Folge hat.

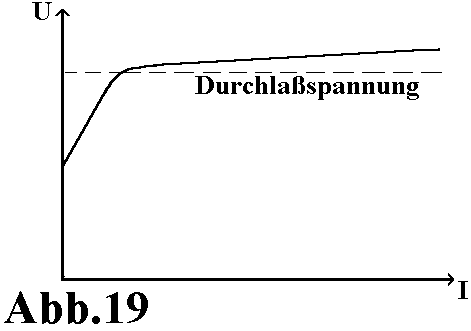
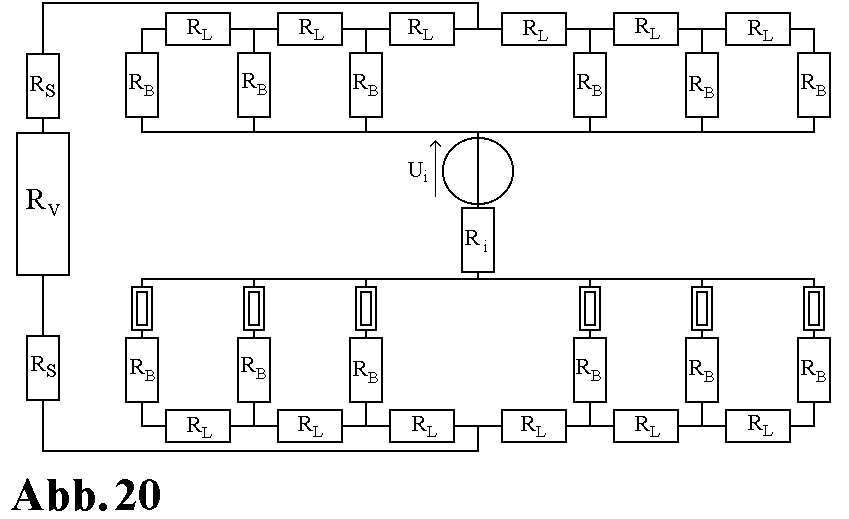
Im Bemessungsbetrieb, also bei einer Drehzahl von 6000 U/min und einem Erregerstrom von 5A ist der gemessene Laststrom um mehr als das zehnfache kleiner als der berechnete Laststrom. Der sehr viel geringere Strom ist auf den Spannungsfall am Bürstenübergang zurückzuführen. Die Patina, die sich auf dem Schleifkörper bildet, hat Halbleitercharakter. Der Widerstand der Bürsten besteht nicht nur aus dem ohmschen Widerstand, der in 2.3.2 berechnet wurde, sondern zusätzlich aus einem Widerstand, der sich mit der Diodendurchlaßspannung vergleichen läßt. In der Abbildung 19 ist der prinzipielle Verlauf der Bürstenübergangsspannung über dem Laststrom aufgetragen. Die Bürstenübergangsspannung ergibt sich aus der Summe der Übergangsspannungen Bürste/Scheibe und Scheibe/Bürste, die jeweils unterschiedlich groß und entgegengesetzt gerichtet sind. Um diesen Einfluß zu veranschaulichen, wird in das Ersatzschaltbild der Versuchsmaschine das Symbol für ein nichtlineares Bauelement eingefügt (Abb.20).

Die induzierte Spannung muß so groß sein, daß die Spannung zwischen den Bürsten oberhalb der Durchlaßspannung liegt, um den angestrebten Laststrom treiben zu können. Eine Vergrößerung der induzierten Spannung bedeutet nach Gleichung (11) eine Erhöhung der Drehzahl, der Durchflutung der Spule oder eine Vergrößerung des äußeren Radius der Induktionsscheibe. Eine Erhöhung der Drehzahl ist aus Gründen der Festigkeit und der Umlaufgeschwindigkeit in Bezug auf die Bürsten nicht zulässig. Die Durchflutung läßt sich bis zu einem Erregerstrom von 8,5A erhöhen, darüber hinaus führt die Erwärmung zur Zerstörung der Spule. Die Vergrößerung des äußeren Radius der Induktionsscheibe führt wiederum zu einer unzulässig hohen Umfangsgeschwindigkeit und zu einer überproprtionalen Kostensteigerung, da quadratisch mit dem Radius das Volumen und damit das Gewicht des Bronzehalbzeugs steigt, aus dem die Induktionsscheibe gedreht wird.

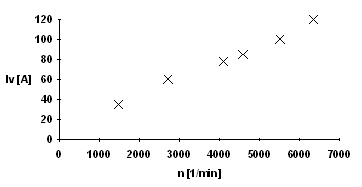
Die folgende Messung wird bei maximal möglichem Erregerstrom und maximaler Drehzahl durchgeführt, um den maximalen Laststrom bestimmen zu können. Die Tabelle 8 zeigt eine Meßreihe bei einem Erregerstrom von 8,5A. Die Messung wird bei stehender Erregung durchgeführt, um die Drehzahl bis auf 6332U/min erhöhen zu können.

Tabelle 8                                                   Diagramm 8

Der maximale Laststrom beträgt 120A bei 6332U/min; das entspricht einer Spannung von Uv=12mV am Shunt. Bei dieser Drehzahl beträgt die induzierte Spannung aus Diagramm 3 durch Verlängerung des Verlaufs Ui=98mV. Der Spannungsfall am inneren Widerstand der Versuchsmaschine beträgt dann URi´ =86mV, woraus sich ein innerer Widerstand von R_i´=717mW ergibt.

Das Gegenmoment M_g, welches an der Welle zum Antriebsrad anliegt, entspricht der Summe aus Reibmomenten und dem inneren Moment Mi. Das innere Moment Mi ist bei Bemessungsbetrieb im Verhältnis zum Reibmoment um den Faktor 80 kleiner. Der Einfluß auf das Gegenmoment ist auf der Drehmomentwaage gerade noch abzulesen. Um feststellen zu können, ob bei Leistungsabgabe ein inneres Moment auftritt, ist es nicht sinnvoll, das Moment an der Welle zu messen und über der Drehzahl aufzutragen. Die Abhängigkeit des Reibmoments von Drehzahl, Stromfluß und Temperatur und das Auftreten von Wirbelstrombremsmomenten ist zu komplex, um aus dem Verlauf Mg=f(n) Rückschlüsse auf das innere Moment zu ziehen.

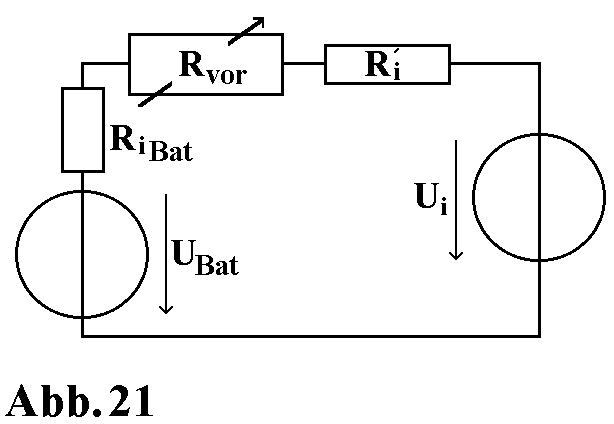
Mit Hilfe einer von außen an die Versuchsmaschine angeschlossenen Spannungsquelle läßt sich eine aufschlußreichere Messung durchführen. Es wird an die Klemmen der Sammelschiene eine Gleichspannungsquelle UBat angeschlossen, die einen möglichst hohen Laststrom durch die Induktionsscheibe treibt. Über einen Stellwiderstand Rvor wird der Strom durch die Induktiosscheibe eingestellt. Bei verschiedenen Drehzahlen wird jeweils das Gegenmoment bei ein- und ausgeschaltetem Last- und Erregerstrom gemessen.

In Tabelle 9 sind die Meßwerte aufgeführt.

Tabelle 9

Das Diagramm 9 zeigt die Funktionen Mg=f(n).

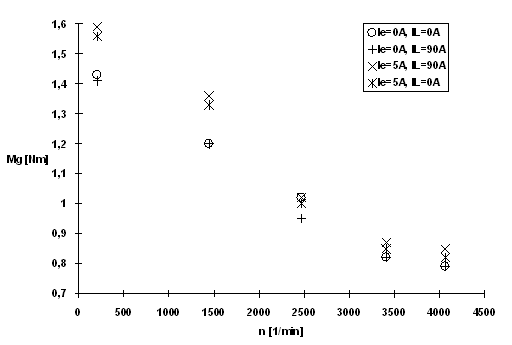
Diagramm 9

Aus den Unterschieden zwischen den Verläufen läßt sich auf das innere Moment schließen. Beim Zuschalten des Laststromes verkleinert sich das Gegenmoment geringfügig. Dies ist auf die Verringerung der Reibzahl der Bürsten durch den fließenden Strom zurückzuführen.

Das Einschalten des Erregerstromes führt zu einer Erhöhung des Gegenmoments. Durch den Vergleich des Gegenmoments bei eingeschaltetem Laststrom und ausgeschaltetem Erregerstrom mit dem Gegenmoment bei ausgeschaltetem Laststrom und eingeschaltetem Erregerstrom wird deutlich, daß die Differenz zum größten Teil aus dem Wirbelstrombremsmoment und zu einem kleinen Teil aus dem inneren Moment besteht.

In Abschnitt 1.4 wird angenommen, daß der rotierend erregte Unipolargenerator deshalb kein elektrisches Gegenmoment erzeugt, weil dieses Moment an der Erregerspule angreift und die Erregerspule mit der Induktionsscheibe verbunden ist. Demnach muß das elektrische Gegenmoment, als inneres Moment bezeichnet, bei stehender Erregung an der drehbaren Erregerspule meßbar sein.

Folgender Versuchsaufbau wird betrachtet:

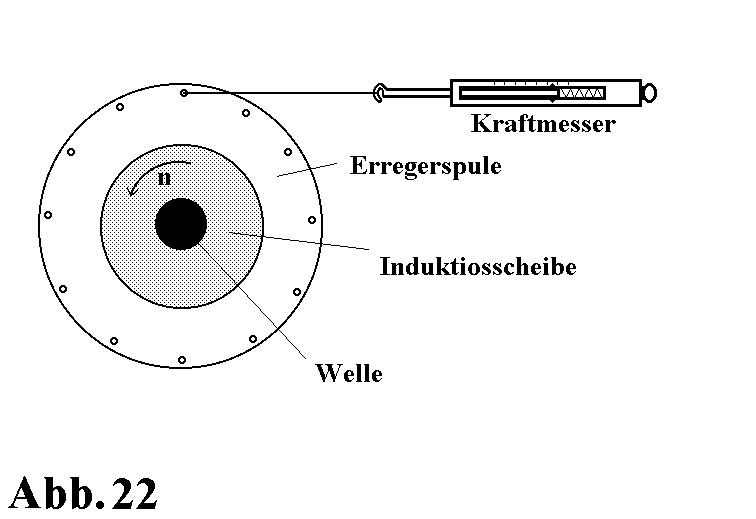
Die Klemmen der Sammelschiene können über einen Stellwiderstand an eine Gleichspannungsquelle angeschlossen werden, so daß ein Laststrom fließt. Die Erregerspule ist frei drehbar. Am Rand der Erregerspulenwand ist ein Kraftmesser derart angebracht, daß er die Kraft in tangentialer Richtung auf die Erregerspule anzeigt und über den Radius von 0,13m das Moment berechnet werden kann (Abb.22). Die Welle der Versuchsmaschine wird bei sehr geringer Drehzahl betrieben, damit das Haftreibmoment überwunden wird. Es wird die Kraft auf die Erregerspule mit eingeschalteter Erregung bei fließendem und nicht fließendem Laststrom gemessen. Bei eingeschalteter Erregung mißt man das Moment auf die Spule verursacht durch Lagerreibung und Wirbelströme. Beim Einschalten des Laststromes von 83A muß sich eine Erhöhung des Gegenmoments zeigen, das sich aus der Lagerreibung, dem Wirbelstrombremsmoment und dem inneren Moment zusammensetzt, wenn das innere Moment an der Spule angreift. Folgende Meßwerte ergeben sich:

Durch das Einschalten des Erregerstromes erhöht sich das Moment auf die Spule wie bereits in Diagramm 4 dargestellt. Das Einschalten des Laststromes wirkt sich nicht auf das Moment an der Spule aus. Die Vergrößerung des Moments wäre meßbar gewesen, da am Kraftmesser ein Teilstrich 0,01N anzeigt, das bei diesem Radius einem Moment von 0,0013Nm entspricht. Nach Gleichung (58) läßt sich das bei einem Laststrom von 83A und einer mittleren Induktion von 0,15T auftretende innere Moment zu M_i=0,0256Nm berechnen. Damit hätte die Anzeige des Kraftmessers bei Einschalten des Laststromes 20 Teilstriche Differenz anzeigen müssen, wenn das innere Moment an der Spule angreifen würde.